“A sample of 1,000 US Algebra # 1 teachers, most rated as “poor” their students’ knowledge of fractions and rated fractions as the second greatest impediment to their students mastering algebra (second only to “word problems)”.       Scientific American

By the time students leave elementary school many have missed out on gaining a deeper understanding of fractions – a  skill critical to the mastery of  Algebra.  But where is the disconnect?

Teaching Math at the elementary level can become siloed.  It is hard to envision a teacher’s role on the fraction continuum.  As teachers we focus on our task at hand – covering our grade level assigned Math standards. Unfortunately children find themselves in the intermediate grades doing fractions rather than understanding them.  This often becomes the beginning of the end of a student’s love of math.                                   

What You Teach Matters; How You Teach It Matters More!

Let’s dive into second and third grade fractions from the perspective of Math standards and the desired outcome.  Here’s a critical second grade fraction standard:

2.G.5: Partition circles and rectangles into two, three, or four equal parts; describe the shares using the words halves, thirds, half of, a third of, etc.; and describe the whole as two halves, three thirds, four fourths. Recognize that equal parts of identical wholes need not have the same shape.

After students are taught equal partitioned parts, part over whole, picture representation, etc…. a beneficial next step would have students moving to the number line showing fraction representations of both one whole and zero.

Let’s look at fractions that land directly on one whole.   Do you see patterns?   What if the denominator is 20, what would the numerator be?    Students can begin to visualize (mental math) the concept of one whole represented as a fraction.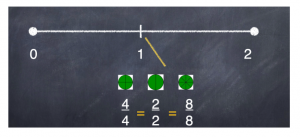

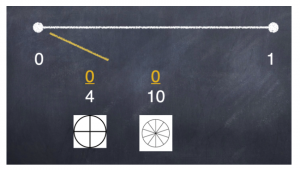
What about fractions that equal zero?   More patterns.

Students leaving second grade with a grasp of equal partitioned parts, part over whole, picture representation, and fraction representation for both one whole and zero are off to a great start in understanding fractions.  

Let’s move onto third grade fraction development.

3.NS.6: Understand two fractions as equivalent (equal) if they are the same size, based on the same whole or the same point on a number line.  

We’ve already started developing the concept of equivalent fractions in second grade:

                                                                              0/4 = 0/10 = 0/100 = 0              

                                                                             2/2 = 10/10 = 50/50 = 1

In third grade we’re honing the concept with other fractions.  Let’s look at one half.   Now we can discuss the relationship between the numerator and denominator.   More patterns emerge.

At this critical point students can use mental math to order the following fractions.         
“Out of 20,000 US 8th graders, when asked whether 12/13 + 7/8 was closest to 1, 2, 19, or 21, only 24% answered correctly.”    Scientific American

There is no longer a need to draw a picture representation to compare which fraction covers more.  Also no need to use cross multiplication.  The desired result becomes children now see fractions as having value and worth by using mental math.

AND going deeper in third grade…

 3.NS.8: Compare two fractions with the same numerator or the same denominator requires reasoning about their size based on the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions.

Comparing ½, ⅓, ¼, ⅕ etc…has students back to picture representations.                                      

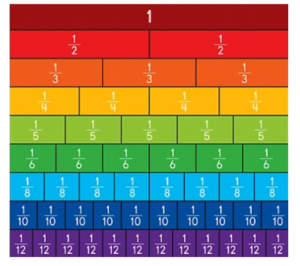
But what if we went deeper with “almost but not quite” fractions?

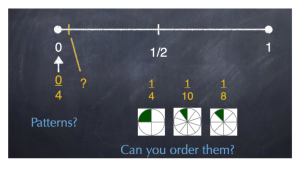
What fraction would land right here – not quite zero?”

Again, as students explore this idea, more patterns emerge.   Then, you can go a step further by ordering  the fractions shown.    Which fraction is closest to zero:  one-fourth, one-tenth or one-eighth?  Why?     More patterns are now created using all the same numerators as outlined in the standard.

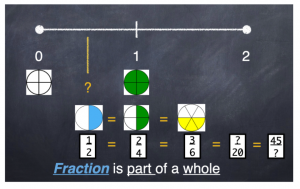
What fraction would land right here – not quite one whole?”

The relationship between the numerator and denominator begins to deepen.   More patterns emerge.  Again, which is closest to one whole: nine-tenths, three fourths, or nineteen-twentieths?  Why?

How about not quite one half?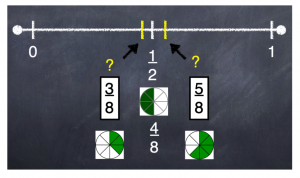 
When students enter intermediate grades, fraction use turns into algorithms, improper/mixed number conversion, etc…  If a deep fraction understanding has developed in 2nd and 3rd grade, students can make sense of these concepts.  Students, who lack an understanding of fractions, find themselves “doing fractions” which results in memorization of rules.   And a dislike for math will emerge.

“Fifth graders’ fraction knowledge predicts high school students’ algebra learning and overall math achievement.”   U Chicago News

 Second and third grade teachers are the key to setting a child’s future in fractions, Algebra and love for math!